A Different View on the Coupon Collector Problem

Oct 27, 2018

Once during a meeting in which we were discussing the Fischer-Yates shuffle someone asked:

How many times do we need to run the algorithm to see every permutation?

The simplicity of this question belies the subtlety of its answer. In fact, you can’t actually answer the question as posed. Because Fischer-Yates is a random algorithm, there is no certain answer. For the sake pedagogy, I proposed to answer another question, more suggestive of the probabilistic nature of the original:

What’s the average number of times I need to flip a coin in order to see both sides?

Enter The Coupon Collector Problem

A classic problem in combinatorics called the Coupon Collector Problem(CCP) captures the setting and solution for tackling both the original question and the one I posed. A coupon here is anything of which there are $m$ distinct types, and the task is to collect at least one of each. For Fischer-Yates, you are collecting all of the $n!$ permutations of a vector of length $n$. For the coin, there is a coupon for each side. The general statement of the simplest version of the problem is then:

What is the average number of coupons that need to be collected in order to get a full set?

We assign an arbitrary order and index $1 \leq i \leq m$. The classic way of getting the result is provided by Wikipedia, which asks you to think about $t_i$, the number of trials to get the $i$-th coupon after you have obtained the previous $i - 1$ coupons of the full set. What’s the probability of getting the $i$-th coupon? Well it’s $p_i = (m - (i-1))/m$. Then the expected number of trials to get the $i$-th is $1/p_i$, just like the expected number of times to roll a 1 on a six-sided die is 6. The total number of trials, then, is calculated by adding up all of these individual exercises in obtaining coupons. Let’s call this total $T$:

$$\begin{align} E[T] &= \sum_{i=1}^m E[t_i] \\ &= \sum_{i=1}^m \frac{1}{p_i}\\ &= \frac{m}{m} + \frac{m}{m-1} + \dots + \frac{m}{1}\\ &= m\left(1 + \frac{1}{2} + \dots + \frac{1}{m}\right)\\ &= m H_m \end{align}$$

The last line above defines the $n$-th Harmonic Number $H_n$. I’ll be honest and say that I really don’t like this derivation. It’s clever and fine, but in general I approach problems like this by reasoning about sums of random processes, and this approach isn’t particularly general. At least, to me, it’s very unsatisfying. In any event, I didn’t answer the original question about Fischer-Yates like this. The rest of this article will take you on a circuitous path towards something that is in the end very simple, and very beautiful. I think it also proves that when all else fails, brute force counting can take you a very long way provided you are obstinate enough to keep going.

Flipping a coin to see both sides

So, let’s get back to the coin. We can model the situation as a set of experiments where we collect successive flips. These experiments generate sequences in which the $n$-th event is $H$ or $T$ and the $n-1$ other events are all either $T$ or $H$ respectively. What would these sequences look like? If we start enumerating the possibilities, we can see patterns appear, depending on how long we run the experiments. For the sequences of length at most $n$,

\begin{align} S_n = \,&HT &&+ TH\\ + &HHT &&+ TTH\\ + &\ldots\\ + &H^{n-1}T &&+ T^{n-1}H.\\ \end{align}

It’s interesting that the sequence of length $k$ is easy to generate from the $(k-1)$-th by simply prepending the opposite of the terminal token, which doesn’t change. Anyway, what do we do with this sum? Well, if we think about $H$ and $T$ as probabilities $P(H) = p$ and $P(T) = q = 1 - p$, then $S_\infty$ better sum to $1$. So let’s check this by collecting terms:

\begin{align} S_{\infty} &= T\left(H + H^2 + H^3 + \ldots\right) + H\left(T + T^2 + T^3 + \ldots\right)\\ &= T\left(\frac{1}{1-H} - 1\right) + H\left(\frac{1}{1-T} - 1\right)\\ &= HT\left(\frac{1}{1-H} + \frac{1}{1-T}\right)\\ &= pq \left(\frac{p+q}{pq}\right)\\ &= 1.\\ \end{align}

On the second step, we’ve inserted the series representation for $\frac{1}{1-x}$ for $x \lt 1$. Since we’re thinking about $H$ and $T$ as probabilities now, we should feel OK about this. Pay special attention to the third step, because we’ll be using it again. Now to calculate $E[n]$ we interpret $S_n$ as a probability density, and evaluate the sum:

\begin{align} E[n] &= \sum_{n=2}^\infty n S_n\\ &=\,2(pq + qp)\, + 3(ppq + qqp) + \ldots m(p^{m-1}q + q^{m-1}p) \ldots...\\ \end{align}

We start the sum for $n=2$ since $S_n$ does not have support for $n < 2$ (i.e. we can’t possibly see both sides by only flipping the coin once). Regrouping a bit, we see that

\begin{align} E[n] &= q\left(2p + 3p^2 + \ldots mp^{m-1} + \ldots\right) + p\left(2q + 3p^2 + \ldots mq^{m-1} + \ldots \right) \\ &= \frac{q}{p} \left(\sum_{i=1}^\infty ip^i - p\right) + \frac{p}{q} \left(\sum_{i=1}^\infty iq^i - q\right)\\ &= \frac{q}{p}\left(\frac{p}{q^2} - p\right) + \frac{p}{q}\left(\frac{q}{p^2} - q\right)\\ &= \frac{p}{q}\left(\frac{1}{1-q} - q\right) + \frac{q}{p}\left(\frac{1}{1-p} - p\right)\\ &= \frac{1 - pq}{p(1-p)}\\ &= \frac{p^2 - p + 1}{p(1-p)}\\ &= 2 + \frac{p^3 + q^3}{pq}\\ \end{align}

For $p = q$ we have that $E[n] = 3$. The average number of times you need to flip a fair coin to see both sides is 3. If $p = 0.25$, then $E[n] = 4.\bar{33}$. If the coin is only 10% fair, then $E[n] \approx 10$. If you’re interested in how it varies with $p$:

Expected number of flips of a coin to see both sides as a function of the bias of the coin.

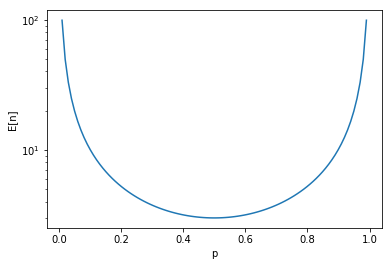
This is maybe a way of estimating if a coin is extremely unfair: build an estimator based on the number flips it takes to see both sides.

Fine for coins, but what about the coupons?

Having solved the problem for $m = 2$, the next thing to do was to try for $m > 2$. First, though, we need to think about the $p_k$, since that’s where it might get hairy. Some options here:

Naive formulation: all equal probabilities, i.e. $ p_i = 1/m$
Singularly hard to get: One distinctive $p_j$, but all other $p$‘s equal
Anything goes: arbitrary $p_i$ subject to $\sum p_i = 1$

The first is a by far the easiest analyze, and will carry us through to the thing I want to show in this article. For the more general cases (and a less casual approach), see Shank and Yang.

So, the most naive approach to the most naive formulation of the problem is brute-force counting. However, once we started to brute-force count for $m \gt 2$ things got immediately out of hand. We needed a more systematic approach. You may have noticed that I used the word generate above. That was a hint. Generating Functions are an incredibly useful tool in the toolbox of the brute-forcing recreational combinatorialist. They’re also pretty fear-inspiring to a lot of people.

Since I’m lazy, I tired of brute force counting the sequences at $m = 3$, but luckily I remembered some advice from Knuth et. al. to use finite automata keep things organized. But before we get to that, it’s first useful to introduce the machinery that we will use when we get there.

The coin redux, this time as a PGF

I’m not going to do justice to generating functions in this space. I recommend Knuth et. al. as a gentle introduction and Wilf if you’re into that kind of thing. But I will give the basic ideas. Imagine that you have a function $G$ that you are able to expand in a power series. You take the convergence of the series as an article of faith, since that mathematical fact is irrelevant to you. All of the benefits of generating functions come by manipulating the series formally. You never actually need to know what the result of the sum. So, we consider $G(z)$:

\begin{align} G(z) &= \sum_{k=0}^{\infty} c_k z^n \lt \infty\\ \end{align}

Suppose you also happen to have a recurrence relation for $c_j = f(\left\{c_i : i < j\right\})$. You may foggily remember how you once you solved differential equations by simply equating coefficients in expansion. You may recall the toolbox for Fourier and Laplace transforms that allowed you to do many computations symbolically. The same thing is going on here. The theory of generating functions allows you to derive from recurrence relation an analytic function $G(z)$, which can be also expanded into the form above. Then, a closed-form version of $c_j$ can read off from the $c_k$ in the series expansion of $G(z)$ on the other side of the equation.

If this is new to you, I’ll say that it really helps to start with simple recursions and work your way up. But, we’re not going to do any of that here. Instead, we are going to take some liberties and just use the machinery. But I am going to go through the calculations in (maybe excessive) detail to help allay some of the fear that people seem to have of GFs.

The first thing we are going to do is realize that any series sum that involves powers of things can be “converted” to a GF by taking some liberties and making some suitable replacements. Why would we want to do this? Well, it all depends on how you choose to interpret the coefficients. In particular, if you interpret the $c_k$ as probabilities, then you actually get something that is formally known as a probability generating function (PGF).

\begin{align} G(z) &= \sum_{k=0}^{\infty} p_k z^k\\ \end{align}

Notice a couple of things here: First, that $G(1) = 1$. Why? well

\begin{align} G(1) &= \sum_{k=0}^{\infty} p_k 1^k\\ &= \sum_{k=1}^{\infty} p_k = 1\\ \end{align}

for everything that we consider to be a probability. Also, notice that

\begin{align} G'(z) &= \sum_{k=1}^{\infty} k p_k z^{k-1}\\ G'(1) &= \sum_{k=1}^{\infty} k p_k = E[n].\\ \end{align}

Now this is useful to lazy amateur combinatorialist. Brute-force counting sequences to calculate $E[n]$ could be replaced by calculating the derivative of the PGF for the process. If only we knew how to create the PGF! Before I show you, let’s observe one more fact about PGFs. Suppose we find ourselves in a situation where we have a PGF that looks something like this

\begin{align} G(z) &= \frac{P(z)}{F(z)}\,\\ \end{align}

where $P(z)$ and $F(z)$ are some analytic functions of $z$. Observe that

\begin{align} F'(z)\,G(z) + G'(z)\,F(z) &= P'(z)\\ \Rightarrow G'(1) &= \frac{P'(1) - F'(1)}{F(1)}\\ \end{align}

This saves us from having to screw around with partial fractions. Now, let’s use all of this on an unsuspecting sum to see if it works. In light of thinking about PGFs, our original $S_n$ (from above) in terms of $T$ and $H$ is worth talking a look at. So, lets make the replacements $H \rightarrow pz$ and $T \rightarrow qz$ and see what happens. This will allow us to promote $S \rightarrow G(z)$.

\begin{align} S &= HT\left(\frac{1}{1-H} + \frac{1}{1-T}\right)\\ G(z) &= p q z^2 \left(\frac{1}{1-pz} + \frac{1}{1-qz}\right) && S \rightarrow G(z)\,,\,H \rightarrow pz\,,\,T \rightarrow qz \\ &= \frac{p q z^2 \left(2-z\right)}{(1-pz)(1-qz)}\\ &= \frac{P(z)}{F(z)}\\ P'(1) &= p(1-p)\\ F'(1) &= 2p - 2p^2 -1\\ G'(1) &= \frac{p(1-p) - (2p -2p^2 - 1)}{p(1-p)}\\ &= \frac{p^2 - p + 1}{p(1-p)}. \end{align}

If you look back at our earlier calculation of $E[n]$, you’ll see the same exact result. So, we accomplished nothing, except to convince ourselves that our machinery works.

The coin again, this time as a finite automaton

We return now to the hint that Knuth et. al. gave us about using finite automata to help generate $S(H,T)$. If we think about the coin problem we’ve been considering, a first stab at at state machine could look something like this.

Flipping a coin to see both sides as a state machine. States Tk and Hk mean that we’ve seen k T’s or H’s respectively.

I’ve labeled the states by number as well. We start in a state $0$ where we haven’t seen a flip yet. Then we start accumulating flips, moving to $T_k$ or $H_k$ initially after a $T$ or $H$, then eventually terminating when we get a flip different from the first flip we saw. Now comes the interesting part. Let’s write down the sequence sum, like we did before, this time using the subscript on $S$ not to index the number of trials, but to index the state $S_n$:

\begin{align} S_0 &= 1\\ S_{T_k} &= TS_0 + TS_{T_k} = T(1+S_{T_k})\\ S_{T_{k}H} &= HS_{T_k}\\ S_{H_k} &= H(1+S_{H_k})\\ S_{H_{k}T} &= TS_{H_k}\\ S &= S_{T_{k}H} + S_{H_{k}T}.\\ \end{align}

Here we have identified $S_{T_{k}H}$ and $S_{H_{k}T}$ as our terminal states. Solving we see that

\begin{align} S_{T_{k}H} &= \frac{TH}{1-T}\\ S_{H_{k}T} &= \frac{TH}{1-H}\\ S & = HT \left(\frac{1}{1-H} + \frac{1}{1-T}\right)\\ \end{align}

This form should be familiar enough now that I don’t have to convince you that this approach worked.

Coupons with Equal Probabilities

We are now prepared to take on the CCP for arbitrary $m$ with all $p_i = 1/m$. As before, define a finite automata to describe the process.

Gathering coupons as a state machine. The state numbers count the number of distinct coupon’s we seen.

Here the states are labeled by the number of distinct coupons we’ve seen. The symbol $X$ takes the place of the $H$ or $T$ and represents the event of seeing a coupon. At the start, there are $m$ ways we can move to state $1$. Once we are in state $1$, there is one way we stay in that state, and $(m-1)$ ways we can move to state $2$. And so on. Then we can read off $S$ as before:

\begin{align} S_0 &= 1\\ S_1 &= m X S_0 + X S_1\\ &= \frac{m}{1-X}\,XS_0\\ S_2 &= \frac{(m - 1)}{1 - 2 X}\,XS_0\\ S_k &= \frac{(m - k + 1)}{1 - k X}\,XS_{k - 1}\\ &= f(X,m)_k\,XS_{k-1}\\ S_m &= XS_{m-1}.\\ \end{align}

Here $f(X,m_k)$ has been introduced to hold the coefficient. Writing down a few terms for small $k$ of the recurrence helps us see a closed form

\begin{align} S_4 &= X S_3 \\ &= X^2 f(3)\,S_2 \\ &= X^3 f(3)\,f(2)\,S_1 \\ &= X^4 \prod_{k=1}^{3} f(k). \\ \end{align}

This leads us to conclude that

\begin{align} S_m &= X^m \prod_{k=1}^{m-1} \frac{m - k + 1}{1 - k X}\\ &= m! X^m \prod_{k=1}^{m-1} \left(1 - k X \right)^{-1}.\\ \end{align}

As before, we make the substitution $ X \rightarrow pz = z/m$, and we promote $S \rightarrow G(z)$:

\begin{align} G(z) &= \frac{m!}{m^m} z^m \prod_{k=1}^{m-1} (1-kz/m)^{-1}.\\ \end{align}

Also, as before, we make the substitution $G=z^{m}/F$ and recall that

\begin{align} E[n] = G'(1) = \frac{m - F'(1)}{F(1)} \\ \end{align}

Then

\begin{align} F(z) &= \frac{m^m}{m!} \prod_{k=1}^{m-1} (1- kz/m)\\ &= \frac{m^m}{m!} Q_m(z)\\ F'(z) &= \frac{-m^m}{m!} \frac{z}{m} Q_m(z) \sum_{k=1}^{m-1} \left(\frac{k}{1-kz/m}\right) \\ &= -\frac{z}{m} F(z) \sum_{k=1}^{m-1} \left(\frac{k}{1-kz/m}\right) \\ &= -z F(z) \sum_{k=1}^{m-1} \left(\frac{k}{m - kz}\right) \\ &= z F(z) \sum_{k=1}^{m-1} \left(\frac{1}{z - m/k}\right) \\ \end{align}

Things are looking very promising. Now we evaluate $Q(1)$

\begin{align} Q(1) &= \frac{1}{m^{m-1}} \prod_{k=1}^{m-1} \left(m-k\right) \ \\ &= \frac{1}{m^{m-1}} \left( (m-1)(m-2) \ldots \left( m - (m - 1) \right) \right)\ \\ &= \frac{\left(m-1\right)!}{m^{m-1}}\\ &= \frac{m!}{m^m}.\\ \end{align}

Interestingly, this means that $F(1) =1$, which also means that $F$ also behaves like a PGF. At any rate, we were now left with

\begin{align} F'(1) &= \sum_{k=1}^{m-1} \frac{1}{1 - m/k}\\ \end{align}

By now, we are tired and we resort to some street fighting, Wolfram Alpha-style, which gives us

\begin{align} F'(1) &= m \left( 1 - \psi^{(0)} - \gamma\right) - 1\\ &= m \left( 1 - (H_{m-1} - \gamma) - \gamma \right) - 1\\ &= m \left( 1 - H_{m-1} \right) - 1\\ \end{align}

using the fact that $\psi^{(0)} = H_{m-1} - \gamma$. Of course, this fact is exactly what Alpha used to give us the answer by re-arranging the sum. Plugging this all in, we finally get

\begin{align} G'(1) &= E[n]\\ &= m - \left(m - m H_{m-1} - 1 \right)\\ &= 1 + m H_{m-1}\\ &= mH_m\\ \end{align}

using $H_m = H_{m-1} + 1/m$. This was our goal.

Now to answer the original question for the equally probable Coupons. In general we can get a one-sided confidence interval for $n$, the number of times we “roll” until success, by using $E[n]$ and Markov’s inequality. If we calculated the variance using the formulas above, we could use Chebyshev’s to get a two sided confidence interval and a tighter bound. Anyway,

\begin{align} P(n > k m H_m) &\leq \frac{E[n]}{k m H_m}\\ &\leq \frac{1}{k}.\\ \end{align}

Setting $1/k = 0.05 \Rightarrow k = 20$. For example, for a six-sided die, for $\epsilon = kmH_m$,

\begin{align} P(n > \epsilon) &\leq 0.05\\ \epsilon &\approx 300 \end{align}

For a permutation of order $6$, the 95% threshold is $\approx 200000$.

Finally, for large $m$,

\begin{align} H_m &\approx \ln{m} + \gamma\\ E[n] &\approx m\left( \ln{m} + \gamma \right)\\ \end{align}

In my weird and twisted way, this is a much more satisfying approach to answer the original question. I’ve always been interested to see how we can apply this to arbitrary finite automata. For instance, I’m curious to use this technique on the KMP Algorithm. I’m a fan of David Eppstein’s Notes on algorithms from long ago in internet time, particularly where he shows a state machine for KMP:

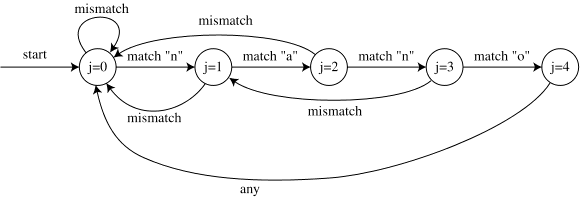
A state machine for matching “nano” with KMP.

Conclusion

Even though I don’t like the canonical explanation, the Wikipedia page on CCP has many useful links. One my favorites in particular is by Flajolet et. al.. That’s a truly systematic approach to the problem, and shows interesting connections to other allocation problems.

Dan Jacob Wallace takes different approach that I enjoyed reading.