Who knew you could generate permutations by walking a graph?

Every so often, I return to my solvers for combinatorial puzzles like Sudoku. There’s another game that has a storied history in computer science, going back to Djikstra’s introduction to backtracking . The problem is Eight Queens. The idea is to find every position of a chess board that can support the simultaneous placement of eight queen pieces. It turns out that there are 12 distinct positions that solve this problem. But if you look at all of the possible solutions you find by backtracking, you actually find 96 solutions. The difference comes from the internal symmetries of the chess board.

You can actually try this game for any number of queens, on any size board. This generalization is call the n-queens problem. The non-distinct solutions for 6 queens on a 6x6 board is shown below.

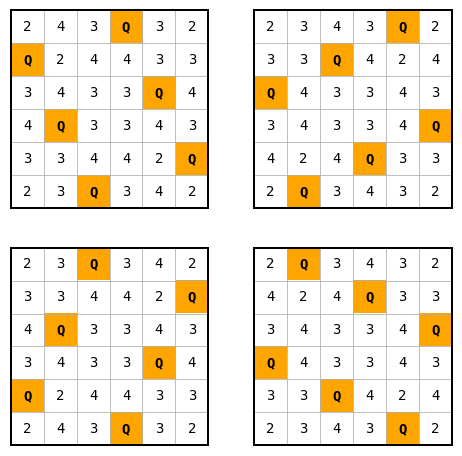
By starting at the top left, you can see that by rotating the board clockwise, you arrive at the top right figure. By flipping horizontally, you arrive at the bottom left figure. By rotating counter-clockwise, you arrive at the bottom right board. There are different ways of dealing with of pruning the non-unique boards, but the last time I played with my solver for n-queens, I tried something I hadn’t thought of before. This post will describe that idea.

Generating permutations is something I’ve always found fascinating. I spent many hours in my youth (and adulthood) writing page after page of permutations trying to find a new way to algorithmically generate them. When I started looking at checking the n-queens solutions for symmetries, I began to think of connections between generating permutations and checking symmetries. This is what I will describe in this post. A jupyter notebook using what’s discussed here can be found on my github. Pruning the backtracking by evaluating symmetries gave a 32x speedup for \(n=6\) (at the end of the notebook).

Symmetries of a Square

So, what’s the symmetry of a chess board anyway? The symmetries of regular polygons are captured by the Dihedral group, \(D_n\). In particular, the symmetries of a n-gon is captured by \(D_n\). A chessboard is an regular 4-gon, so it’s symmetries are captured by \(D_4\).

What do I mean that \(D_4\) captures the symmetries of a square? \(D_4\) is generated by clock-wise and counter-clockwise rotations of 90° and reflections about the vertical, horizontal and diagonal axes of the square.

A generating set captures the idea of a specific set of transformations that are sufficient to generate the group. If you’ve never seen this before, the systematic exploration of this is what group theory is all about. I recommend Carter for a friendly and geometrical introduction. For an accessible introduction to generating sets, I recommend Keith Conrad’s notes. Keith has a wealth of good reading in his blurbs.

There is a visual and systematized way of encoding all of these relationships for a particular group, called a Cayley graph. Cayley graphs use a particular generating set of transformations (like reflection and rotation above), and show how you can arrive at every symmetry of your starting point by sequentially applying transformations. The Wikipedia article on Cayley graphs actually has a graph for \(D_4\) in the example section

To see what’s happening here, start at the F labeled \(e\). By applying \(a\), we go up along the arrow and we get an F that has been rotated 90 degrees in the clockwise direction. If you then follow the dotted line up and to the left, you are applying a horizontal reflection \(b\). If you moved back along the dotted line, you would go back to where you were before, and algebraically you would be at \(abb\). But since \(bb = 1\), i.e. two reflection across the same axis take you back to the same place, you end up algebraically back at \(a\). Rotations don’t work like reflections. Two clockwise 90 degree rotations don’t take you back where you started. Instead, \(aaaa = 1\). This is why the arrows have directions, and why there’s an outside square and inside square of arrows, that give \(aaaa\) to get you around to where you started.

So, what does this have to do with my original interest in symmetries of n-queens? Well, say we start with a configuration of queens, such as in the top right solution above, how would I algorithmically take that board on a tour of every symmetry it has under \(D_4\)? If you look at the Cayley graph above, you can imagine starting at \(e\) and applying \(a\) and \(b\) in a way to take us to every other node. But how do we do this in a systematic way? How can we only visit each node once?

In computer science terms, we’re asking of there exists at least one Hamiltonian path in that graph, and if so, how do we find it. Finding Hamiltonian paths in graphs is one of the classic NP-complete problems of computer science. We don’t actually know if every Cayley graph is Hamiltonian, but the famous Lovász conjecture posits that they are. And, the Lovász conjecture has been proven for almost all cases of finite Cayley graphs. If you look at the graph above, a Hamiltonian path isn’t too hard to see:

Since the end \(aab\) and the beginning \(e\) are not related by \(a\) or \(b\), then this can’t form a Hamiltonian cycle. Can we find one? Remember that we only used two of the many possible transformations to make that graph. What about if we used others, what would happen? Consider the Cayley of \(D_4\) using \(b\) as before, but now using reflection along the SE to NW axis, which in our terms would be \(c = ba\), a 90 degree clockwise rotation followed by a horizontal reflection:

While tracing a path around, remember that \(bb=cc=e\), whereas before \(aa\neq e\) (which was a vertical flip). Also, in the top right, going from \(bcb\) up via \(c\) would give you \(cbcb\), but this is the same as \(bcbc\), since you can always multiply both ends by the same thing. Notice also that in writing \(c = ba\), the order of \(a\) and \(b\) matter. Except for \(D_1\) and \(D_2\), the generators of \(D_n\) do not commmute. The fact that generators don’t commute in general makes the Cayley graph a hall of mirrors when you are trying to find a single path through it.

At any rate, in this Cayley graph, you can immediately see the circuit we can take to evaluate all of the symmetries of a n-queens position. Typically in an n-queens solver you represent the board as an \(n \times n\) matrix. In this setting, evaluating reflections is as simple as swapping matrix entries seven times. In my solver, every time I find a solution by backtracking, I quickly check the board against solutions that I’ve saved before. Doing this at the time of finding a solution greatly speeds up the backtracking since it substantially prunes the tree.

Hamiltonian Paths for Permutations

As I mentioned before, I’ve always been interested in generating permutations. As we saw, we could find a slick way to visit all of the the elements of \(D_4\), but if we want permutations, we still have \(n!-2n\) to figure out.

Just as the symmetries of a square are captured by \(D_4\), the \(n!\) ways of arranging \(n\) objects is captured another group, which is called the symmetric group \(S_n\) on \(n\) objects.

This time \(e\) is in the middle right at \(1234\). Edges that have a dot are rotations in the direction of the dot: \(1234 \mapsto 4123\). These rotations are counterclockwise by the dots. Edges without dots are swaps of the first and second items: \(1234 \mapsto 2134\). If we walk along the edges from \(1234\) towards \(2134\), we can see that we are getting closer to a Hamiltonian path on \(S_4\):

This is almost right. But wrong because we had to flip the two orange edges between \(1423\) and \(4231\) and between \(3142\) and \(2314\). Technically it’s wrong because the orange edges are \((1432) = (4321) \neq (1234)\). But this is encouraging.

I really like this representation of \(S_4\). If you notice, the central diamonds all have red and green on one side of the square, and yellow and blue on the other. If you look at the larger squares above and below the diamonds, you see that in each permutation, red and green are on opposite sides of across the permutation. If you look at the red and green around \(1234\), \(4123\), \(2134\) and \(1342\), you notice that they are mirror images of each other despite the fact that the link between the sides is a transposition of items \(1\) and \(2\). The yellow and blue don’t obey the mirror symmetry. To me this representation shows how much crazy scrambling goes on in permutations, as well as the many kinds of parity symmetries we can observe in \(S_4\).

As another way of visualizing permutations, we can look at the notation used for cycles and swaps. Over \(S_3\), a 3-cycle that simultaneously moves the first to the second, second to third, etc, we write \((123)\). If we write out the \(3! = 6\) 3-cycles of \(S_3\), we get: \((123),(132),(213),(231),(312),(321)\).

Some of these do the same thing, for instance \((123)\) and \((231)\), but \((123)\) and \((132)\) do something different. But what’s clear from writing it out that we have a cycle for each actual permutation of 3 objects. Because of this, we conclude that the cyles of any permutation group generates the group. Taking the cycles as the generating set has an obvoius disadvantage when you are trying to algorithmically generate permutations: you have to already have the permutations to make the generating set. It would be nice to be able to use a more compact set of generators. Luckily this is possible.

Generating permutations exhaustively requires \(n!\) amount of work. For large \(n\), this can get literally astronomical. I mentioned the Fischer-Yates shuffle in the post on the Coupon Collector. If you are not familiar with that algorithm, it uniformly generates random permutations.

for(int i = 0; i < n; i++)
    swap(a[i], a[rand(i, n-1)]);

Part of the reason I have spent so much time thinking about F-Y because of Skiena, where he asks why the following does not generate uniformly random permutations:

for(int i = 0; i < n; i++)
    swap(a[i], a[rand(0, n-1)]);

Analyzing the algorithm, in particular why it generates uniformly random permutations, and why this second snippet doesn’t, is my favorite interview question. Maybe I will post about that later. But for now, taking a step back, why do we think that generating permutations by swaps would even work?

Well we’ve seen that swaps have a role to play in the Cayley graph above for \(S_4\). But that generating set also uses cycles. F-Y doesn’t use cycles, just swaps. Using a similar formalism to the way we write cycles, we can also write swaps. In particular, we write the exchange of the first and second elements as \((12)\). A moments reflection tells us that: \((1234) = (12)(23)(34) = \sigma_{12} \sigma_{23} \sigma_{34}\). I wrote the \(\sigma\)‘s because we are going to watch them in action and don’t want to create too much confusion with paranthesis. Note also that the permutations apply by acting on the right. We will also use letters rather than numbers to keep the confusion at a minimum

Which gives us the same result as the cycle \((1234)\). So, cycles are products of \(n-1\) swaps. Since cycles generate symmetry groups, that means that swaps also generate the symmetry groups. We can now see why F-Y is a good idea, or at least why it might work.

There are \(\binom{n}{2} = \frac{n(n-1)}{2}\) swaps for \(S_n\). So, if we want to use swaps to algorithmically generate permutations, then we only have to do \(\binom{n}{2}\) work finding the generators before we can start making permutations. This saves a lot of work. But we can do even better. It turns out that for any \(n \geq 2\), \(S_n\) is generated by \((12)\) and \((12...n)\). A proof is found at Keith Conrad’s notes. This means we can use the same generating set for any \(n\), and the only upfront work we have to do is in creating the cycle. These cycles are the ones used to make the Cayley graphs of \(S_4\) above.

If you’re wondering how one could even get started making the Cayley graph for \(S_4\), one thing to think of is that each time you apply \((12..n)\) to a permutation, you can only apply it \(n\) times before you end up back where you started. This means that if we can construct \(n!/n = (n-1)!\) of these \(n-\)orbits distinctly, then we’ve found all of the permutations of \(n\). Then we just need to find another generator(s) to link the \(n-\)orbits together to get a complete Cayley graph. That’s exactly how I made the graphs above. Start with \(1234\) and make it’s \(4-\)orbit, then pick another permutation not in that orbit, and repeat this until you are out of permutations. Then look for pairs of individual permutations that match up according to \((12)\). Arrange them in an aesthetically pleasing way and there’s your graph.

Before we go any further, know that the definitive reference on generating permutations (and most every other common combinatorial object) is Knuth 7.2.1.2 (AoCP V42A). He gives the relevant algorithms and also a very thorough history of the topic.

Back to using swaps. One day a few years ago I was writing out permutations, and I found the following pattern. For any \(n\), write out the \(n-1\) swaps in columns. Start with \(e\), for the case of \(S_4\), that’s \(1234\). Move the permutation to the right using the swap in the column until you get to the end of a row. When you get to the right side of the table, go down with the first swap \((12)\). Then go back across the table the other direction until you hit the left side of the table. Then go down with the last swap of the set. Keep this up until you get back to \(e\). This process is shown below.

This works for \(S_4\) because there are 4 permutations per row, 3 complete cycles from left to right and back again, and two rows per cycle. Thus we have \(4*3*2 = 4!\) items. When I first wrote this down, the excitement, as with most discoveries in amateur combinatorics, was short lived. After some research I learned that this was figured out in the 1960’s. This algorithm is called the Johnson-Steinhaus-Trotte (JST) solution to the motel problem. The motel problem comes from Martin Gardner’s Time Travel and other Mathematical Bewilderments:

Mr. Smith manages a motel. It consists of n rooms in a straight row. There is no vacancy. Smith is a psychologist who plans to study the effects of rearranging his guests in all possible ways. Every morning he gives them a permutation. The weather is miserable, raining almost daily. To minimize his guests’ discomfort, each daily rearrangement is made by exchanging only the occupants of two adjoining rooms. Is there a simple algorithm that will run through all possible rearrangements by switching only one pair of adjacent occupants at each step?

It turns out this problem is even older than that. McGuire describes the history of this problem dating back to the 17th century:

Suppose there are n bells being rung, numbered 1,2,3,…,n in order of pitch, number 1 being the highest. When the bells are rung in order of descending pitch 1, 2, 3, … , n, we say they are being rung in rounds. A change in the order of the bells, such as rounds 1 2 3 4 5 being changed to 2 1 4 3 5, can be considered as a permutation in the symmetric group on five objects. In the years 1600–1650 a new craze emerged where the ringers would continuously change the order of the bells for as long as possible, while not repeating any particular order, and return to rounds at the end. This game evolved into a challenge to ring the bells in every possible order, without any repeats, and return to rounds.

McGuire plausibly claims that the method above was actually discovered by bell-ringers in the 1650’s. JST only solves one variant of the large topic of change ringing. McGuire provides a nice history of this and ties it back to Hamilton paths on Cayley graphs. The Simons Foundation has a nice video on the topic.

Knuth gives a number of examples of changes.